Altitude and Dynamic Error in TPE and CUBE
Total Propagated Error (TPE) and Combined Uncertainty Bathymetric Estimator (CUBE) help automate data cleaning and filtering. This paper discusses the effect of using altitude in place of heave for survey data processing and that of using error estimates in TPE and CUBE for both variables. Final hydrographic data quality is examined. Total Propagated Error (TPE) and Combined Uncertainty Bathymetric Estimator (CUBE) are designed for use with hydrographic survey data to minimise subjective user intervention and help automate data cleaning and filtering. With the trend in hydrographic surveying towards objective estimation of data quality, these methods rely heavily on error estimates generated by the geo-referencing and motion-compensation systems installed on hydrographic survey vessels.
Background
Previous studies have demonstrated the usefulness of including an instantaneous estimate of horizontal pos-ition error in TPE and CUBE1. These studies proved that use of a priori error estimates was not robust, and methods are now in place to read and make use of computed RMS position error estimates. At the same time, a new trend in bathymetric survey data processing has emerged, the use of Altitude on the ellipsoid in place of vertical displacement, or Heave.
Applanix POS MV (Position and Orien–tation System for Marine Vessels) is an GPS-aided Inertial Navigation System specifically designed to produce an accurate estimate of echo-sounder position and orientation on the ellipsoid in all vessel dynamics. The system computes all motion variables, including latitude, longitude, altitude, heading, pitch, roll, and heave. It is the altitude that has become an area of focus and it is now possible using inertially-aided RTK to consistently compute high-bandwidth Altitude with sub-5cm results and to produce an even more robust solution by making use of post-processing techniques.
This paper will identify the effect of using Altitude in place of Heave, and that of using error estimates in TPE and CUBE for both variables. Final hydrographic data quality will then be examined.
Discussion
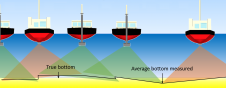
The basic components making up the measurement of the vertical in hydrographic survey are illustrated below. Shown is the relation of the GPS antenna to water line, geoid, chart-datum and sea bottom. It is, after all, the depth in which we are interested. The important thing to stress here is that if we know the relation of the echo sounder to the ellipsoid and the ellipsoid to the chart-datum we eliminate the need for dynamic draft.
TPE aims to automate the processing of hydrographic data and therefore it is extremely important to pay attention to how error estimates are weighted. A focus of this paper is error estimates for the vertical.
“In order to obtain the total variance for the final depth (D final) of an individual sounding, one must sum all of the variances that are associated with depth uncertainties.These variances are a combination of the total measured depth variance and the reduced swath depth variance."
The variance carrying subscript (d) is the total variance of the measured depth, and the variance carrying subscript (D) is the total variance of the reduced depth. Measured depth is corrected for Heave. Heave is equal to the vertical displacement of the vessel, to a zero mean level, at a given instant in time. The reduced depth is corrected for Tide.
Heave RMS is currently a function of wave height and not necessarily an objective error estimate of the measurements making up the Heave function. In order to use Heave in bathymetric processing knowledge of dynamic draft is required. There is no standard method of measuring or estimating dynamic draft error. Conventional inertial instruments that measure heave cannot measure long periods of swell. Therefore a component of unmeasured motion and error estimation exists in the total variance of the measured depth when Heave is applied.
Errors associated with tide measurement are related to the measurement at the gauge itself and spatial de-correlation related to the distance of the gauge to the survey area. Tidal measurement variance is described in the equation below.
The preddoes not include measurement of changes in water level due to seiche, wind-driven tide or other phenomena which can cause slowly varying change in water level.
This paper will show visible benefits in plots of depth surfaces when Heave is replaced by post-processed ellipsoidal Altitude. The uncertainty for Altitude is computed by the Inertial Navigator and can be input into TPE. The uncertainty for Tide and dynamic draft fall out of the equation. The remaining uncertainty will be in the transform–ation of ellipsoidal Altitude to the chart datum.
Heave should only be replaced by Altitude when the positioning system is capable of providing sub-5-centimetre accuracy, or as otherwise required by the user. As mentioned above, this means that post-processed kinematic (PPK) positioning data should be used, see illustration. There are several benefits to be gained by GPS/Inertial post-processing. Real-time kinematic (RTK) often suffers from radio-link issues and rarely do we find 100% of the acquired position data to be in fixed-integer, narrow-lane mode. In post-processing, data gathered at the reference is made directly available to the GPS re-computation and fixed integer will always be achieved if the rover is within 20 to 30 kilometres of the reference. A smoother can be applied to inertial-position data, the effect of which will be to significantly reduce error in any periods where GPS data is lost. A smoothed best estimate (SBET) of position is produced. SBET data provides sub-5-centimetre Altitude with a high degree of confidence.
Data Analysis
CARIS HIPS 6.1 has been used in this analysis. This version has been engin-eered to accept SBET data, which not only contains latitude, longitude and altitude but also a RMS value for each positional attribute. CARIS HIPS 6.1 also has options for loading the RMS data. The use of these values in the TPE computation provides a more rigorous determination of overall error budget. It also aids the process of automated data cleaning by identifying areas of varying uncertainties rather than the processor having to identify these through investigation. It will also highlight areas of concern currently concealed in the TPE computation.
A dataset acquired offshore California in 2005 was used in this analysis. The survey vessel was the MV Quicksilver, 32 feet in length and 3-foot draft. The vessel was equipped with a ResonSeabat 7125 and an Applanix MV320.Real-time navigation was based on OmniStar HP. All positioning raw data was saved in Applanix POS MV and reprocessed in Applanix POSPac. The survey area was near shore, in an area heavily influenced by tides. The data was processed in four ways.
Case 1: Standard CUBE Processing with Heave and a priori estimates of error
Note data anomalies especially visible in the lower portion of the plot. These inconsistencies have magnitudes of up to two metres and result from busts in the application of Tide and dynamic draft. On the right-hand side of Figure 3 is the CUBE uncertainty surface. This is mostly flat due to the fact that static, a priori estimates of error have been used. The a priori estimates of error are taken from manufacturer’s specifications.
Case 2: Standard CUBE Processing with Heave and dynamic estimates of error
Case 2 look very similar to the Case 1 plot, but dynamic estimates of error have been used in TPE for position. Dynamic estimates of position error are calculated as a RMS derived in the Applanix POS MV Integrated Inertial GPS Navi–gator. Depth surface remains flawed due to tide and datum busts; however, the uncertainty surface reflects changing uncertainties for horizontal pos–ition that increase with water depth. The effect of dynamic uncertainties on depth surface is minimal because pos–itions were derived in post-processed kinematic (PPK) mode. Very accurate positioning is the result. The dynamic error estimates (from the PPK) were close to the a priori ones. Previous studies have demonstrated the effect of GPS satellite outage and the difference in depth surfaces when dynamic error is not used1.
Case 3: Altitude substituted for Heave with a priori estimates of positional error
Case 3 shows the effect on depth surface of using Altitude instead of Heave. A dramatic improvement in data coherency is seen. It is important to note that human processor intervention in Cases 1 to 3 was approximately the same. The result, however, is clearly better using PPK Altitude. On the right-hand side of Figure 5 is the CUBE uncertainty surface, mostly flat and not showing any centralised problematic areas, thanks to use of static, a priori estimates of error taken from the manufacturer’s specifications, as in Case 1, except for Altitude instead of Heave.
Case 4: Altitude substituted for Heave with real estimates of positional error
Case 4 again shows the effect on the depth surface of using Altitude instead of Heave. A dramatic improvement in data coherency is seen. Again, it is important to note that human processor intervention in Cases 1 to 4 was approximately the same. The result, however, is clearly better using PPK Altitude. As in Case 1 compared to Case 2, no big difference in uncertainty surface is seen when dynamic error is used instead of manufacturer’s a priori estimates. This, as discussed above, is because data quality from PPK was excellent. However, there are two small, localised areas where there is an increase in the uncertainty layer. As already said, the use of dynamic error will clearly highlight localised areas of sensor problems as opposed to a priori estimates from the vessel file.
IHO Order
Perhaps the most striking benefit of the application of Altitude and Dynamic Error in TPE and CUBE is the IHO order classification that may be derived with equal processor/operator effort. The remaining illustrations show IHO order classification based on depth difference of a tie line with the main survey swaths across the survey area. This was calculated by constructing a surface and comparing a tie line. Comparing a check line to the constructed CUBE surface is essentially a measure of repeatability and reliability.
Concluding Remarks
This paper clearly identifies the benefits of using PPK Altitude in place of Heave, and discusses the pros and cons of applying continuously updated sensor uncertainties. It was seen that the new implementation of TPE computation would allow for modelling changing sensor uncertainties throughout data collection. With auxiliary sensors, including the use of swath sonar, associated uncertainties constantly vary and it is prudent therefore to use these derived values in TPE computation to achieve a more robust result. More significantly, in the cases presented in this paper the affect of Altitude in place of Heave on depth surface is extreme. It was shown that, with a similar effort in human processing, a much better result could be obtained with Altitude.
Editor’s Note: This article was first presented at US HYDRO ‘07 and is published here with kind permission of the organisers.
Notes:
1Canter, Lockhart & Collins Caris 2005, Error Estima-tion in Positioning and Orientation Systems.
2The Study of Total Propagated Error in Hydrographic Surveying, Corey Collins, Dep. of Geodesy and Geomatics Engineering, Uni-versity of New Brunswick, March 2004.
Value staying current with hydrography?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories from the world of hydrography to help you learn, grow, and navigate your field with confidence. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired by the latest in hydrographic technology and research.
Choose your newsletter(s)