GPS for Global Tidal Measurements

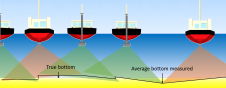
Hydrographers require accurate three-dimensional positions of the survey vessel and typically use differing methods for resolving the horizontal and vertical components. GNSS, such as the Navstar Global Positioning System (GPS), have become the dominant horizontal positioning system for hydrographic operations, whereas tidal estimation is the foremost method used in determining vertical positioning. The tidal estimation method integrates a water level measurement at a remote location with a predicted propagation of the tidal wave, to establish a sea surface level at the desired location. This paper investigates a new method using GNSS as an aid in improving these water level estimates on a global level.

Aided GPS has been available in three basic forms: Differential Code Phase GPS (DGPS), Satellite Based Augmentation Systems (SBAS), and Real-Time Kinematic Carrier Phase Tracking GPS (RTK). DGPS systems work primarily through corrections to the user observed pseudo-ranges. They are inexpensive, reliable and can provide vertical accuracy as good as 3 metres at 95 per cent confidence. SBAS (EGNOS, WAAS, MSAS) operate on a continental region and utilise a network of reference stations to provide orbit, clock and regional Iono/Trop corrections with accuracy similar to that of DGPS. RTK Kinematic GPS positioning integrates both the signal code and carrier phase to establish a horizontal (and vertical) position with an accuracy of 0.02 metres at 95 per cent confidence, but at considerable increase in cost and effort. DGPS is range limited to several hundred kilometres from the Reference Station before 'spatial decorrelation' errors become dominant, while RTK operations are typically limited to 10 to 15 kilometres or so. SBAS systems are regionally based.

Tidal Estimates
On tidal estimates, the United States National Ocean Service (NOS) states: "The allowable contribution of the error for tides and water levels to the total survey error budget falls between 0.20 metres and 0.45 metres (at the 95 per cent confidence level) depending on the complexity of the tides." Tidal estimation, while certainly the most practical means of determining vertical positioning available to date, has certain unfortunate limitations. Foremost, tidal estimation errors are sufficiently large that they often become the dominant source of error in depth measurements. Another critical limitation is the lack of data redundancy.

Tidal Errors
Tidal errors are difficult to detect. In addition, the hydrographer has little guidance concerning the reliability and accuracy of the tidal correctors being applied to the soundings, except for fundamental analysis derived from cross-line comparisons or survey junctions. NOS states that discrepancies should not exceed 3 per cent in areas of irregular bottom and moderate depth. The US Army Corps of Engineers declares that a mean cross-line difference of 0.18 metres is expected during hydrographic surveys of dredged channels. It is unfortunate that such beneficial guidelines for cross-line depth comparisons provide us with little insight into the complexity of tidal error.

RTG GPS Aiding
C-Nav Real Time GIPSY (RTG) is a world-wide GPS aiding system. It offers an accuracy improvement of about 1 order of magnitude compared to traditional DGPS, with ease of use and robustness similar to that of SBAS or IALA beacon-aided GPS. The RTG technique is a proprietary real-time version of the Jet Propulsion Laboratory (JPL) GIPSY correction methodology developed by NavCom Technologies, Inc. The original requirement for GIPSY was to position spacecraft in orbit around the Earth, for which precise positioning is needed but local reference stations are not possible.
The RTG correction methodology minimises position errors in five ways:

1. Accurate orbit correctors establish satellite position at the time of transmission
2. Accurate satellite clock correctors minimise satellite clock errors
3. Dual frequency processing eliminates ionosphere delays
4. Extended carrier smoothing reduces multi-path and receiver noise
5. Kalman filtering estimates residual troposphere delay and other errors and corrects for them

Globally Corrected GPS
One interesting aspect of this methodology is that all errors attributed to the receiver and its location are resolved at the receiver, while all errors attributed to the space vehicles and the GPS control system are resolved on a global scale. Thus, there is no spatial decorrelation of the solution. Because of its universal applicability, the RTG method is referred to as 'GcGPS' - i.e., 'Globally corrected GPS'. The receiver hardware is based upon NavCom's SF-2000R receiver, which consists of a dual frequency geodetic grade GPS receiver, an integral L-band receiver module for collecting satellite broadcast GPS correctors, and a processor to calculate real-time position. It is capable of automatically switching between eighteen different modes of operation to determine the highest accuracy solution available. The normal operating mode of C-Nav utilises RTG correctors in the dual frequency 3D mode, the results of which are presented in this paper.

Vertical Accuracy
The most widely accepted accuracy requirements for hydrographic surveys are those put forth by the International Hydrographic Organisation in Special Publication #44. The 4th edition, published in 1998, gives the required depth and position accuracy as a function of survey order and water depth. The IHO recognises four survey orders. Order 1, the most common, is the only one examined in this article.
IHO gives the required Order 1 depth accuracy as: AD = [a2 + (b * d)2]0.5

Where:'AD' is the allowable depth error in metres
'a' is a constant depth error
'b' is the factor of depth dependent error
'd' is the water depth in metres
For Order 1 Surveys (a, b) = (0.5, 0.013)

IHO states that the depth error should include: "...all contributing errors which include among other things:

• Measurement system and sound velocity errors
• Tidal measurement and modelling errors
• Data processing errors"

Total depth error is primarily comprised of (a) and (b) above, or sounding errors and water level errors respectively. Although both typically have approximately equal magnitudes, the hydrographer may form any balance between the two, provided that the total depth accuracy is adequate. Data processing errors are normally minuscule when compared to the tidal component. Assuming that sounding and tidal errors are equal and not correlated and that the processing error is negligibly small, the required water level accuracy can be estimated as: Awl » (AD2/2)0.5
Where:Awl is the required accuracy of the water level estimate with reference to the sounding datum.

Tidal Estimation
RTG altitude measurement could provide significant benefits for water level estimation providing that its vertical accuracy is clearly established as adequate. Utilising both tidal estimation and RTG altitude measurements to estimate water levels may have several advantages to the hydrographer such as:

• Establishing an upper bound for the water level estimate when tide station implementation or zoning is complex
• Providing a reliable check for tidal blunders
• Providing useful feedback to those performing harmonic analysis of tides
• Providing an adequate source of water level information in case of tide station failure

DataSet Study
In order to establish RTG global vertical accuracy, data was collected from five statically located SF-2000RM receivers placed at surveyed points well dispersed across the globe. The receivers used NavCom firmware, Version 13.1. Data collection took place over a period of 25 (5-30 July 2003) to ensure that results would represent system performance in a variety of conditions. The X, Y, and Z errors of each receiver position with respect to the survey position were determined at each epoch. Mean errors, standard deviations and errors at various confidence levels were determined. Further data regarding the monitoring stations is presented in Table 1.
Antenna locations were surveyed using the JPL Automatic-GIPSY post-processing application. GPS receiver raw L1/L2 C/A code and phase measurements for a 24-hour period were recorded and converted to RINEX observation data files. These files were then submitted to the Auto-GIPSY process at JPL. The Auto-GIPSY process uses the RINEX files and IGS precise ephemeris to calculate antenna position with millimetre level accuracy.

Data Processing
The data was filtered for invalid NMEA data strings and incomplete epochs. At each epoch the X, Y, Z errors with respect to the surveyed position were tabulated for each receiver. The errors were sorted by magnitude and represented as percentiles. The mean errors and standard deviations for each axis were also determined.

Accuracy
Raw C-Nav data were analysed and the results are shown as Tables 2 and 3. It is expected that these levels of accuracy may be moderately improved through further analysis and selective filtering.
The data shows that the vertical accuracy of the recorded positions using the RTG methodology is approximately 0.35 metres at the 95 per cent confidence level. Furthermore, the accuracy varies by only a small amount world-wide.
Table 4 shows the required tidal estimate accuracy for Order 1 surveys as a function of water depth, assuming that sounding accuracy and tidal accuracy are equal and the processing error is negligible. The empirically determined vertical accuracy of RTG and estimated accuracy of tide measurement and zoning given by NOS are overlaid for reference.
Table 4 illustrates two interesting points. First, determining water level using tidal estimation in shallow water is unsatisfactory for Order 1 surveys if the tides are complex. Second, C-Nav RTG, while not as good as the best tidal estimate, is generally adequate for estimating the water level during IHO Order 1 surveys.

Conclusions
C-Nav, incorporating RTG dual frequency receivers, currently provides a world-wide vertical accuracy of 0.35 metres at the 95 per cent confidence level, a precision useful to hydrographers. This data may be valuable for improving the accuracy of water depths, particularly in areas where the implementation of tide stations or zoning is complex.