Precise RTK GPS Water Levels

As more people adopt RTK GPS technology for measuring water levels, the issue of ellipsoid-geoid separation is increasingly being discussed. This article outlines various projects undertaken to calibrate this separation, and presents information to consider when using RTK GPS for measuring relative to an orthometric (geoid) datum.

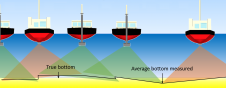
RTK GPS is increasingly being used for measuring water-level corrections during hydrographic survey, as for water levels in general. Measuring this third vertical dimension usually requires local site calibration to correct for separation between WGS84 ellipsoidal height and geoidal elevation, enabling conversion of WGS84 heights to orthometric heights such as mean seal level or chart datum. Most existing survey data relates to one such datum. Over small distances, the separation between ellipsoid and geoid can be approximated using a calibrated incline plane. Site calibration is explained, with examples of different incline plane models.

Incline Plane Technique
GPS measurements are made relative to the WGS84 ellipsoid, which is a perfect ellipsoidal approximation of the Earth’s surface. Orthometric
heights are affected by localised topographic variations and differ significantly (> 30m) from the WGS84 ellipsoid. Although many people are successfully using soundings relative to the WGS84 ellipsoid, in reality most users of hydrographic data still require soundings relative to an orthometric datum. To convert between these two surfaces survey marks in the region need to be available with both WGS84 and orthometric levels. The number of marks required will depend on the accuracy required for the water-level corrections, the amount of existing information and the budget available for surveying extra marks. The survey marks are used in a ‘least squares adjustment’ to best fit an incline plane between the two surfaces. It is shown in this article that for the size of the areas surveyed here the incline-plane method well approximates ellipsoid-geoid separation. For other areas with larger variations in the geoid, or covering a larger area, more than one incline plane model may have to be made to optimise accuracy.

Calibration Results
Four different incline plane models have been made at the New Zealand locations seen in Table 1 and Figure 1. Incline model calibrations can include horizontal adjustments, but the focus of this article is on the vertical fine-tuning of the WGS84 ellipsoid to the geoid. The result of such a calibration is an origin of the incline plane, separa
tion between the surfaces at the origin, plus a slope to the north and east (Table 1). If a geoid model is being used as well (such as AUSGEIOD98, DMA 10x10, EGM96, GEIOD93, GEIOD99 etc.), this calibration will better calibrate the geoid model for the location. For this research incline plane models have been made using Trimble’s Geomatics Office land surveying package, for use with
Trimble’s HydroPro hydrographic survey and navigation software for measurement of water levels. The Geomatics Office software was used because land surveying was required to collect extra control data. Additional control data required surveying orthometric marks to give them a WGS84 ellipsoidal
height, and this was done using a combination of RTK GPS and fast static surveys using a Trimble 4000 base station and Trimble MS750 RTK GPS rover. If coordinate pairs were available to make the incline plane model then this could have been done solely in HydroPro. Table 1 shows the magnitude of the values calculated for each site, to give readers an idea of typical results around the central North Island of New Zealand. It is expected that globally these values will vary significantly. For some locations a geoid model has been calibrated and for others not.
It can be seen in Table 1 that the use of a geoid model has made the constant adjustment for the Lake Rotorua and Rotoiti (Figure 2) sites much smaller than for Lake Tarawera (Figure 3), even though they are only 18km from each other. Using the geoid model, although 1.39m in error over the Lake Rotorua and Rotoiti site, is still 3.09m more accurate than without the model. Effective difference between a geoid model being used or not is expected to be dependent on the accuracy of the geoid model and the size of the site. For larger sites, more investigation is required to determine if the geoid and geoid model fit the theoretical incline plane model, or if the surfaces are excessively undulating.
For the Mount Maunganui sites the aim was to have a calibrated incline model for surveying of the Port of Tauranga navigation channel and the Mount Maunganui beaches. In the case of the first survey there was no time beforehand to collect additional control information around the site, so exist-
ing survey data had to be used. Survey marks from the Land Information New Zealand (LINZ) geodetic database that had both ellipsoid and orthometric
heights were downloaded (www.linz.govt.nz) and used to make a first approximation of the incline plane (Figure 4). A subsequent dense GPS control survey over existent orthometric marks was made (Figure 5) that significantly improved the model. This later incline plane model is the author’s most accurate to date.

Residual Errors
Comparing the models for Mount Maunganui it is quite surprising to see the accuracy of the model based on a small number of spare control points, as compared to the more rigorous model (Figure 4). Assuming the RTK GPS-derived model is close to the true value, the residual errors in the LINZ data model are quite small, considering the effort put into the model. Downloading these few LINZ control points and creating a model took a few hours. Surveying, checking and calculating the more accurate RTK GPS model took closer to a day and a half.
The survey purpose is to determine how much effort is required to create an accurate incline plane model. For example, when comparing survey information in a harbour with accurate dredge-survey monitoring done by another survey party, the closer water-level corrections are to the true datum the better. If the aim is to look at beach erosion or monitor dredge spoil dispersal then the situation is slightly different. Using the LINZ-based incline plane model will give very accurate relative results between surveys. It is only when trying to compare with soundings collected using a different method, such as traditional tide gauge, problems may arise.

Lake Water Levels
An advantage of using RTK GPS water-level corrections is that the level at the soundings is being measured rather than from a remote site such as a tide-gauge. In harbours, rivers and lakes there can be significant variations in water levels and without an impractical number of gauges true water surface can never be properly resolved.
Figure 6 shows water levels measured over the surface of Lake Tarawera. There is a significant gradient from one side of the lake to the other, as well as possible variations around rivers flowing into and out of the lake. The cause of the water level variation has not been investigated at this stage.

Discussion
For much of the work done by the University of Waikato relative differences are more often important than absolute levels. The Coastal Marine Group is often more focused on physical processes over time than accurate absolute depths. Examples are bar-rip migration, movement of bedforms, dredge spoil dispersal, channel infilling and delta migration. This means that for much of our work, including projects that may be research-orientated and only partially funded, these less accurate geoid models are still a viableoption. A variety of different scenarios for dealing with the ellipsoid-
geoid separation have been used since the Coastal Marine Group began using RTK GPS for water-level corrections in 2000. Extra care is required when using these lesser accuracy incline models, and some validation immediately around the survey site is recommended.
Future proofing of the data is an important issue to consider when using incline plane models to correct RTK GPS heights to a local datum. For example, when a series of surveys is done using a lower accuracy incline plane model for a project that is only concerned with relative changes between surveys. After the series of surveys the requirements of the project to investigate relative changes may be answered, but what about future uses of the data? If there is a 0.1-0.2m constant error in the incline plane model, then this data cannot be compared accurately to historical or future data. Therefore, as an investment in the future use of the data it may have been a better option to spend more time initially to calibrate the site.
Another option for approaching the survey just mentioned is to ignore using local datum. If relative changes are all that is required, then the final product of the survey could be WGS84 coordinates. This will answer the questions on relative changes but does not introduce any errors based on poor ellipsoid-geoid separation modelling. In this scenario the burden of the conversion to a local datum is therefore put onto future users of the data. In cases where there may be no future uses of the data this may be a good option. The question of who should convert the soundings to a local datum is most likely to be driven by economics. Where is it most economically feasible to make the conversion: during the survey or in the future, if and when the data is to be used again? It is probably safe to assume geoid models and conversion tools will improve in the future and conversion may become easier.
Since the conversion between WGS84 and orthometric heights will always contain some degree of uncertainty, perhaps it is prudent to create water-level files and final sounding products with both orthometric and WGS84 heights. This will ensure that future users of the data can investigate the accuracy of prior geoid conversions as well as apply their own, possibly more accurate, models. It is a real concern that soundings may be stored with poor geoid models that may never be capable of more accurate conversion, as better geoid modelling becomes avail-able. For this reason, metadata on how the soundings were converted (e.g. incline model parameters) should be a minimum requirement of any RTK GPS water-level corrected survey.