Tide Models for Hydrographic Surveying
Computer models replace tide poles
Hydrographic surveying has become a highly sophisticated operation, with GPS for accurate fixing of position, acoustic technology for mapping the sea-bed either side of the survey vessel, and on-board computer systems to automatically process the data. But the corrections made for tide are in many cases still done using methods that date back to Captain Cook's days in the late 18th century. These methods may be adequate for places where the tide does not change much from place to place, or if the tidal range is small. But in places where the tide varies widely, the accuracy of tidal corrections can become a significant factor in the overall accuracy of the survey. One solution is to use a local-area tide model in which the hydrodynamics of tidal flow are solved in a computer model. This can allow accurate tidal corrections to be done on-board in real-time.
In the days of Captain Cook, hydrographic surveying was done using a sextant and a sounding line. These days, we use GPS and echo sounder, with an attendant increase in accuracy and speed of execution. But one thing that had to be done by Captain Cook and must be done today is correcting measurements for the tide.
Tide-pole Technology
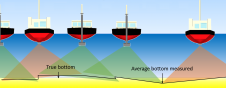
Traditionally, correction for tide has been done by landing sailors at various strategic locations on the coast, each with a tide-pole - a pole with graduated markings - and having them read the level every 15 minutes over the period of the survey. From these measurements a map is drawn called a ‘cotidal chart’, showing how the tide varies over the region. Indeed, this method is still used today. However, there are some places where the tide changes so rapidly that this method is inadequate, its accuracy being much less than that achieved by sophisticated survey instruments such as GPS and multi-beam sounding systems.
Highly Variable Tide
An example of a place where the tide is highly variable is Cook Strait, between the North and South Islands of New Zealand (Figure 1). On the south-west coast of the North Island, the M2, or semidiurnal lunar tide has almost zero amplitude, yet within a 30km its amplitude is up to 0.6m. Further, the time of high tide varies widely. These two factors make it very difficult to make accurate corrections from tide-pole observations.
Tide Models
One solution to the problem is to use a tide model in which individual tidal constituents are determined on a grid. To obtain the tide at a particular time and place, the constituents are interpolated and a tide forecast is done. There are two sorts of tide models available: global tide models and local-area tide models. Global tide models are available from the internet and they are free. Local-area tide models must be developed for the area under consideration and use a global tide model for their boundary conditions.
Global Tide Models
There are many global tide models available. Most are derived from data from the oceanographic satellite TOPEX/Poseidon (Figure 2) and provide up to thirteen of the main tidal constituents, on a rectangular grid with spacing of between 0.25 and 1¼ of latitude and longitude. The models use ground-truthing from tide-gauges and hydrodynamic considerations to a greater or lessor extent, and this governs how accurate they are close to the coast. For remote locations such as around New Zealand such global models are not accurate near the coast; they also give quite erroneous results for Antarctica, mainly because TOPEX/Poseidon does not cover the region below 65¼S.
Local-area Models
Local-area models solve shallow-water equations using tidal constituents from a global model for deep-water boundary conditions. They also take account of ocean-loading tides (deflection of the Earth’s crust in response to the tide) and Earth tides (deflection of the Earth’s crust in response to the direct gravitational attraction of Sun and Moon). The accuracy of a local-area tide model depends upon the accuracy of local bathymetry and shoreline. Usually, these can be defined in much smaller detail in a local-area model than in a global tide model, and hence the accuracy is much enhanced.
The Model Grid
Two sorts of model grid are used in local-area models: rectangular or unstructured. In a rectangular grid the computational nodes are equi-spaced in each direction. The disadvantage of this is that, to properly model the coastline the spacing over the whole grid must be a few hundreds of metres. This makes for very large models requiring large computing resources. An alternative is to use an unstructured grid whose spacing varies with the proximity to the coastline (Figure 3). In the grid shown, the triangles are roughly equilateral in shape and their area is roughly proportional to the average depth beneath them. This has two advantages: the triangles are small near the coast where it is shallow, and large in the open ocean where it is deep, producing a natural nesting of the grid; the tide takes the same time to travel over large triangles as it does over small triangles. This makes for a high degree of numerical stability in the computations.
Time-stepping or Harmonic?
There are two types of computational scheme: time-stepping or harmonic. In the time-stepping method, the solution is progressed one step at a time. The disadvantage of this method is that the model must be run for a sufficient time to enable the various tidal constituents to be separated from each other. For most situations this involves running the model for long enough to simulate 207 days. Then the solution must be further processed to extract the tidal constituents at each node. On the other hand, the harmonic computational scheme solves for each tidal constituent in turn. However, whereas time-stepping can use rather simple mathematical techniques to solve the equations, the harmonic scheme results in a huge matrix equation that must be solved iteratively.
Model Validation
Before using the results of a local-area tide model for correcting surveys, the model needs to be validated by comparing its results with those of one or more nearby tide gauges. These gauges can also be used during the survey to measure and correct for storm surge, which is the response of the ocean to changing atmospheric pressure and wind.
The Future
In recent years Land Information New Zealand, has commissioned three hydrographic surveys that used local-area tide models for tidal corrections: in Cook Strait (Figure 1), in Foveaux Strait (Figure 3), and in Western Ross Sea, Antarctica. In each case, thorough testing of the model was required before it was approved for use but in each case, for one reason or another the survey would have been unsuccessful had it not been for the tide model. In the case of the Western Ross Sea survey, a tremendous storm carried away all the ground-based measuring equipment, leaving the tide model as the only means of making tidal corrections.
Value staying current with hydrography?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories from the world of hydrography to help you learn, grow, and navigate your field with confidence. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired by the latest in hydrographic technology and research.
Choose your newsletter(s)