Multi-beam Error Management
New data processing trends in hydrography
The hydrographic community has tumbled headlong into a data boom. Hundreds of single-beam soundings are now replaced by millions of high-resolution multi-beam swath soundings. This boom is not free from the problems inherent in how data is to be handled by ever-shrinking staff and ever-increasing demands for ways to store, process and archive gargantuan datasets. Luckily, modern computer hardware and processors can handle the load. However, there is still the issue of affording resources for traditional data processing, where each sounding is scrutinised. What new software approaches are being developed to automate processing? This article describes one new and innovative approach for preparing data for products the accuracy of which is known with a high degree of confidence and archived with the data. This can then be passed on to the user, whose application could very well depend on knowing the data uncertainty.
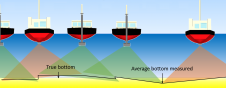
High-resolution multi-beam surveys carry with them the most advantageous tool for quality assurance-redundancy. Redundancy in beams, pings and swaths, along with specific knowledge of the sounding errors, allows a new approach to resolving the best estimation of depth at a given location and attributing each depth with realistic uncertainties.
Propagating Vertical Error
Forward-error prediction, resulting in a total propagated error or TPE, can be used for estimating horizontal and vertical accuracy values by accounting for and propagating the estimated random error contributions from all sources. For soundings obtained by vertical Single-Beam Echo Sounders (SBES) this propagation is relatively straightforward, as described by Myres (1990). To estimate total propagated depth error the following must be taken into account:
- sounder measurement error (a function of detection method in the case of Multi-Beam Echo Sounders (MBES))
- sound speed correction errors (refraction errors for MBES)
- dynamic draught measurement errors (includes static draught, load changes, squat and settlement)
- heave measurement errors
- tide or water-level errors (including gauge precision, constituent quality, spatial extrapolation, synchronisation of gauge with measurements, etc.).
For MBES the process is somewhat more complex (Hare et al., 1995). One must also take into account errors in roll-and-pitch measurement on depth and errors in determining transducer-head misalignment angles. Figure 1 shows the estimated vertical error for a selection of multi-beam systems.
Propagating Horizontal Error
To estimate TPE for position the following must be taken into account:
- sounder measurement error (can be ignored for SBES)
- refraction errors (bending of beams in MBES)
- roll, pitch, and heading errors
- positioning system errors
- sensor coordinate offset errors
- transducer-head misalignment errors (all three orientations)
- latency errors between sensors.
Errors in each of two dimensions (e.g., latitude and longitude) can be combined to create a one-dimensional radial error, such as Circle of Equal Probability (CEP) or distance root-mean-square (drms). For both depth and position errors the TPE can then be scaled to approximate the 95% confidence level.
Traditional Focus on Sounding
Understanding the magnitude of data uncertainty as described above for hydrography, or any other purpose, is of fundamental importance in developing robust and appropriate methods for processing data into information required to update a chart or for decision support. Traditionally hydrographic practise has focused on each sounding, asking "Is this sounding valid?" All soundings (subjectively) judged valid are then considered equal and the shoalest in any area is taken as representative. While ‘safe’, this method ignores the known uncertainties of the data. We know that each measurement is to some degree uncertain and that combinations of them increase the potential uncertainty. Therefore, no sounding is truly ‘valid’ beyond reasonable doubt. All soundings have error and some have more than do others. Sounding errors are not created equally.
New Focus on Depth
An alternative approach is to recast the fundamental question as: "How well do we know the depth here?" Although simple, this distinction is fundamental: we focus on the datum of interest, the depth, rather than the means of determining it, the sounding. And we include a statement of our certainty about the determination.
Using the CUBE
The Combined Uncertainty and Bathymetry Estimator (CUBE) algorithm (Calder and Mayer, 2003) is an attempt to utilise understanding of the uncertainty of soundings in a processing scheme for high-density MBES data that answers to the alternative question of depth and uncertainty. Starting with the Hare-Godin-Mayer error model for MBES (Hare et al., 1995), it attributes each sounding with an estimate of vertical and horizontal uncertainty. It then estimates the true depth at a fixed point in space, given only the noisy soundings from the data-stream and their associated uncertainties.
Robust Algorithm
Robustness is enhanced by a ‘Multiple Hypothesis Tracker’ sub-component that allows the algorithm to accumulate evidence for a depth estimate from all soundings that are consistent within their estimated uncertainty and exclude those that are inconsistent, assigning them to a separate estimate. The hydrographer can then consider the algorithm’s depth reconstructions from these estimates and determine whether they are consistent with the observed soundings, hydrographic prior knowledge, and each other. Any inconsistencies are resolved before the modified areas are recomputed to yield the final estimates of depth in a dense grid over the survey area. The outputs are summarised by a surface representation of the depths and associated uncertainties.
Allowing Automation
CUBE handles most common problems in MBES survey processing; however, it cannot solve all problems. Human intervention is always required to resolve intelligently circumstances in which data is incomplete or does not correspond to the hydrographer’s understanding of the seafloor, and where the algorithm cannot or does not correctly determine the depth estimate to report. In this case it is the hydrographer’s task to correct algorithm perspective on the data by manually selecting another hypothesis, as in Figure 2, or by marking a ‘designated sounding’, considered from that point to represent absolute truth. Since these cases are typically limited in extent, overall operator workload is significantly reduced (Calder and Smith, 2004), as shown in the graphs in Figures 3 and 4. However, by refocusing the process on depth rather than soundings another challenge arises: if we have depth estimates and uncertainties with which to qualify them, how do we leverage these to provide better information, faster and cheaper and using fewer resources?
The Navigation Surface
The data flow now uses a grid data product to represent the bathymetric part of a hydrographic survey. The Navigation Surface (NS) method of representation of bathymetric surveys was developed at the University of New Hampshire by LT Shep Smith (NOAA) and replaces the traditional ‘selected sounding’ dataset representation of a survey with a collection of grids. Each grid is built (by CUBE methods) to represent the best estimate of the true depth of the water at precise locations across a survey area, while maintaining significant hydrographic detail where required. The NS is a Digital Terrain Model (DTM) of the seafloor that is optimised for safety of navigation (Smith et al., 2002). A statistical model is created directly from processed data, fully attributed with vertical and horizontal error. The model created is a best estimate of depths, not soundings. The error attribution methodology presented here is through CUBE. The NS approach, combined with CUBE, is the real step forward in processing multi-beam data.
Optimised Seafloor Model
The model of the seafloor consists of a high-resolution bathymetric grid with an uncertainty value assigned to each node on the grid. The model is then optimised to preserve the least depths over significant features. For each node an uncertainty value is computed which becomes an integral part of the model. The distribution of the points around the mean is combined with the predicted uncertainty of each measurement to form an overall uncertainty model. The basic principle is that the NS database is populated with the highest resolution reconciled surface model that the source measurements (survey data) can support.
Products from NS
Using an NS as a database a variety of products (contours, selected soundings, depth areas, DTMs, etc.) can be produced or extracted. Products can be created based on the suitability of the source data to produce a level of detail appropriate for the intended use. Most often this is directly related to the desired scale of the product. Figure 5 demonstrates surfaces of varying resolution generated in response to user requirements and fully attributed with errors. For Electronic Nautical Charts, this would be ‘navigational purpose’ and the attribution of an uncertainty or ‘confidence’ value of depths by populating the CATZOC field. The grid product is constructed in such a way that it is equivalent in terms of safety of navigation to the traditional ‘points-and-lines’ product currently used, which includes the traditional ‘smooth-sheet’, also known as a ‘field-sheet’ or ‘fair-sheet’. Hence the grid may be certified as the legal source of the bathymetric information for the construction of traditional nautical charts.
Emerging New Methods
New technology gives us the potential to deal with the challenges posed by new methods for high-resolution hydrography. However, if we are to take advantage of the density of data that we now collect we can no longer afford to ignore or bypass fundamental uncertainties associated with our survey data. The techniques outlined here allow us to estimate and utilise the uncertainty of the data, opening the way to new products and services while maintaining and enhancing the fundamental requirement of hydrography: to support safety of navigation.
Further Reading
- Hare, R.M. (1995). ‘Depth and position error budgets for multi-beam echosounding’, International Hydrographic Review, Monaco, LXXII(1), March 1995, pp 35.
- IHO. (1998). IHO Standards for Hydrographic Surveys, 4th Edition, April 1998, Special Publication N¡. 44 (S-44), pp 23.
- Calder, B.R., ‘Automatic Statistical Processing of Multi-beam Echo-sounder Data’, Int. Hydro. Review, 4(1), 2003.
The submitted article included many references; the author is very willing to send interested readers the article with references included.
Value staying current with hydrography?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories from the world of hydrography to help you learn, grow, and navigate your field with confidence. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired by the latest in hydrographic technology and research.
Choose your newsletter(s)