RTK Tide Basics
One of the fastest emerging trends in hydrographic surveying is the use of the vertical component of RTK GPS to determine real-time water level corrections. There are currently several district offices of the US Army Corps of Engineers using this technique in place of conventional tide measurements.The main purpose of this article is to explain some of the basics behind the technique (without getting overly technical) and to point out some of the benefits and drawbacks to the method.
The Basics
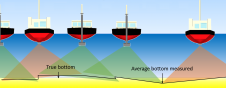
Looking at Figure 1, let’s define the following terms:
For simplicity, I am ignoring the heave-pitch-roll of the vessel and am assuming the vessel is in a pleasantly static, upright, condition. For the following examples, we have calibrated our echosounder to the ‘static water line’ and our sounder is outputting depths based on this level. From conventional hydrographic surveying, we can define a simplified Chart Sounding (CS) from our example as:
CS = RD + D - Tc (1)
Based on our drawing, we can see that:
A + D = Tk + H + SEP (2)
Solving for the RTK Tide component gives:
Tk = A + D - H - SEP (3)
Substituting this into our formula for the chart soundings results in:
CS = RD - A + H + SEP (4)
We have everything we need to determine the Chart Sounding in real time without having to resort to a conventional tide reading. Note also that the Dynamic Draft measurement has cancelled itself out of the formula and is not necessary to compute the chart sounding! (More about that later on.) The key to getting this technique to work is to accurately determine SEP (the height of the Chart Datum above the Ellipsoid Reference).
Determining Separation
In Figure 2 I have provided some values to each of our parameters. In this first example, there is no draft correction as the vessel is in its ‘static’ condition. (D = 0)
Using our conventional formula (1), we get the Chart Sounding:
CS = RD + D - Tc
CS = 10 + 0 - 2 = 8
In order to determine the separation of the Chart Datum above the Ellipsoid Reference, we can just transpose our observed values into formula (3), using the conventional tide value as our RTK tide value.
Tk = A + D - H - SEP
SEP = A + D - H - Tk
SEP = 6.5 + 0 - 3 - 2 = 1.5
So at this location, the Chart Datum is located 1.5 above the Ellipsoid Reference. It is important to note that this value may change over a large survey area. The height of the Chart Datum above the Ellipsoid Reference can change over a short distance, especially in areas of complex tides. We may be safe using it as a constant for a local survey about a pier, but we wouldn’t want to rely on a single separation value used over a large area.
The Tide Comes In
In the next example (Figure 3), our vessel is still sitting statically at the dock but the tide has risen another 2.0. We would also expect that A (Height of RTK Antenna above the Ellipsoid Reference) and RD (raw depth from the echosounder) would also rise by the same amount. Using the formula to determine our RTK Tide correction gives the following:
Tk = A + D - H - SEP
Tk = 8.5 + 0 - 3 - 1.5 = 4
It follows that our Chart Sounding is:
CS = RD - A + H + SEP
CS = 12 - 8.5 + 3.0 + 1.5 = 8
In this case, the computed RTK Tide (Tk) equals the conventional tide correction (Tc) and we can obtain the chart sounding in real time without any delay. It would be possible to carry out a statistical comparison between the Tk and Tc values for each sounding to see exactly how the two values compare.
The Vessel Squats
In this example (Figure 4) the vessel is underway. Due to ‘squat and settlement’, the vessel is sitting 0.2 lower than its normal static position. We will assume we have a method to determine this change in the vessel’s dynamic draft. The tide remains the same as in the previous example. Since the vessel has ‘dropped’ 0.2, the values for A and RD will also drop by the same amounts. Using the formula to determine our RTK Tide correction gives the following:
Tk = A + D - H - SEP
Tk = 8.3 + 0.2 - 3 - 1.5 = 4
It follows that our Chart Sounding:
CS = RD - A + H + SEP
CS = 11.8 - 8.3 + 3.0 + 1.5 = 8
As the vessel squats and the water level changes, we still get the correct Chart Sounding. As long as we can measure the dynamic draft value, the computed RTK Tide should equal the conventional tide correction (Tk = Tc)
No Draft Measurement
Having been on hundreds of different survey vessels, I can honestly state that less than 50 per cent of them ever apply any kind of dynamic draft correction. They either don’t have the means to automatically measure the draft or they haven’t taken the time to manually correct for the draft. (Don’t shoot me, I’m only the messenger.) Figure 5 shows the known values. In this case we have the same values as the last example, except that we are going to have to use D = 0, since we don’t have any input for the value. Using the available parameters:
Tk = A - H - SEP + D
Tk = 8.3 - 3 - 1.5 + 0 = 3.8
Tk ¹ Tc
We compute our Chart Sounding:
CS = RD - A + H + SEP
CS = 11.8 - 8.3 + 3.0 + 1.5 = 8
Notice that the computed RTK Tide no longer equals the conventional tide correction! In all of our previous examples, Tc = Tk. It gave us the ability to compare our RTK Tide with the conventional tide correction value and to generate statistics on the variation between the two.
That is no longer the case. We have now computed some kind of ‘pseudo-tide’ value. This value, when used in the computation for the Chart Sounding, gives the correct result. If we look at the chart sounding using conventional methods, we will see that we get a result that is in error by an amount equal to the missing draft correction:
CS = RD + D - Tc
CS = 11.8 + 0 - 4 = 7.8
If you don’t have the ability to include the dynamic draft correction, the RTK Tide method will still give you a correct sounding, whereas the conventional method will result in an error.
Varying SEP
When working in a large survey area we can’t treat the SEP as a constant. In the chart shown in Figure 6 we have determined SEP values at four different locations in our area and can plainly see that it varies. Any RTK Tide application that works over a large area must somehow incorporate the ability to change the SEP value based on the location of the vessel. In our software package (HYPACK MAX), we use a Kinematic Tidal Datum file that contains the SEP values for the corners of gridded rectangles. Based on the position of the vessel, it determines which rectangle it lies in and then computes an SEP for the vessel position based on its distance from each corner of the rectangle.
Incorporating Data
The height of the RTK antenna above the reference ellipsoid may only be reported once per second by your GPS, whilst the echosounder is updating over fifteen times per second. If the boat is in a dynamic environment (waves), we need to be able to model the movement of the sensors between the RTK updates. A heave-pitch-roll sensor is used in almost all RTK applications. Working with numerous clients, we have developed two different approaches to rectify this problem.
In the first approach, shown in the top half of the Figure 7, we assume the RTK Antenna Heights to be the ‘gospel truth’ and use the information from the Heave-Pitch-Roll sensor to reconstruct the movement of the sensors between the one-second updates. In a perfect world, the vessel motion between the RTK updates would be a perfect fit. Unfortunately, it isn’t a perfect world and we are sometimes forced to ‘stretch’ the predicted motion, using the RTK elevations as anchors for the stretch.
In the second approach, shown in the bottom half of the graphic, we use the RTK Antenna heights to determine a ‘Normalised Heave Reference’ and then apply the exact vertical movement for the sensor as computed from the heave-pitch-roll data. The rationale for this approach is as follows.
Your heave-pitch-roll sensor outputs a ‘heave’ value that is the height of the sensor above a normalised heave plane. If you place the sensor on the floor for a couple of minutes and then place it on a shelf 1m high, the heave will change to 1m. After a couple of minutes (depending on the settings in your unit) the heave will slowly drift back to 0. The 1m shelf has become the ‘normalised’ heave reference and your heave is now referenced about this level.
In the second approach, we average the RTK z-values for a specified time period before and after each RTK update to determine the ‘normalised heave reference. We then apply the exact heave-pitch-roll motion relative to this value. In this approach, the RTK Antenna heights are our ‘guide’ and the heave-pitch-roll data is the ‘gospel truth’.
In calm waters there isn’t any noticeable difference between the two techniques. In dynamic conditions, the second approach seems to give a better result. With RTK GPS sensors now outputting Antenna Heights Above Ellipsoid at 10Hz, the possibility now exists to eliminate the heave-pitch-roll sensor and use just the RTK GPS updates.
In Summary
- The trend towards using RTK GPS for real-time water levels is growing
- The RTK Tide method generates correct Chart Soundings whether you measure the dynamic draft or not
- You can only compare the RTK Tide and the conventional tide if you accurately measure the ship’s dynamic draft
- The separation between the Chart Datum and the Reference Ellipsoid should only be considered a constant for a very small survey area
- You have to have a heave-pitch-roll sensor to determine the sensor movements between one-second RTK updates
Download rtk_tide_basics_1.pdf
Download RTK Tide Basics 1
Download rtk_tide_basics_2.pdf
Download RTK Tide Basics 2
Download rtk_tide_basics_3.pdf
Download RTK Tide Basics 3
Download rtk_tide_basics_4.pdf
Download RTK Tide Basics 4
Value staying current with hydrography?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories from the world of hydrography to help you learn, grow, and navigate your field with confidence. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired by the latest in hydrographic technology and research.
Choose your newsletter(s)